Scientific Focus

Quantitative analysis of programs

• Numerical invariant generation for safety

• Formal methods for Software Engineering

• Reactive systems: synchronous design

• Compilation: scheduling, termination of programs

Why ?

• Reactive systems

• Proving full correction

• Because termination is related to scheduling

The big picture

Given a program

//N>0
i = N;
while(i>0)
{
   j = N;
   while(j>0) j--;
   i--;
}

Compute a model (or intermediate representation)

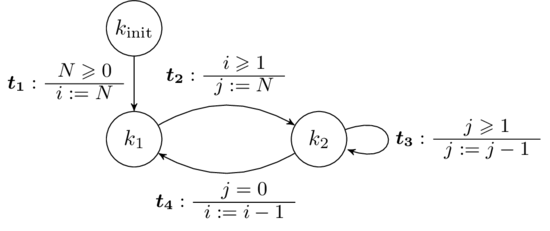
Prove termination of the model.

From Hoare rules to ranking functions

• Hoare rule for total correctness:
  • \(\frac{\{t=z \mbox{ and }{t\in D} \mbox{ and } P \mbox { and }B\}S\{P\mbox{ and }t<z\mbox{ and }t\in D\}}{\{\mbox{P}\} \mbox{while B do S done} \{\mbox{not B and P}\}}\)
  • with \((D,<)\) well founded

• In our case:
  • \(D=(\mathbb{N}^d,<_{lex})\) and
  • we look for \(\rho(k,-)\) positive and strictly decreasing.
  • we need (numerical) invariants \({\cal I}_k\)!

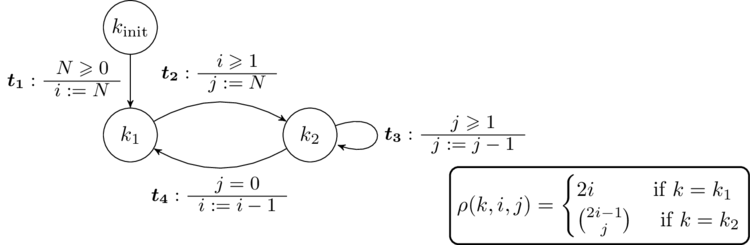
Algorithm (Alias, Darte, Feautrier, Gonnord 2010) :

• From the program representation, we build a system of constraints:

  • \(\rho\) is positive : \(\rho(k,\vec{x})\geq 0\) on \({\cal I}_{k}\)
  • \(\rho\) is decreasing : \(\vec{x'}-\vec{x^{}}\in \tau \Rightarrow \rho(dest,\vec{x'})-\rho(src,\vec{x^{}})<0\)

• We transform it into a Linear Programming instance

• We solve.

Issues of the first implementation

Rank tool on compsys-tools.ens-lyon.fr

• applicability: only numerical programs
  • abstraction of all non-numerical statements
  • not enough!

• scalability:
  • complexity is \(O(nbvars*nbcontrolpoints*dim)\)
  • LP instances are too big
  • using slicing is not enough

Fighting against scalability : overview

• [WST14] (with F. Pereira, Brasil): realworld loops are simple !
  • slice and pattern-match

• [Submitted to PLDI] (with D. Monniaux, Grenoble) : only a few assignments in a loop actually matter !
  • Consider loops as single transitions and only heads of loops
  • Compute incrementally the LP-problem.

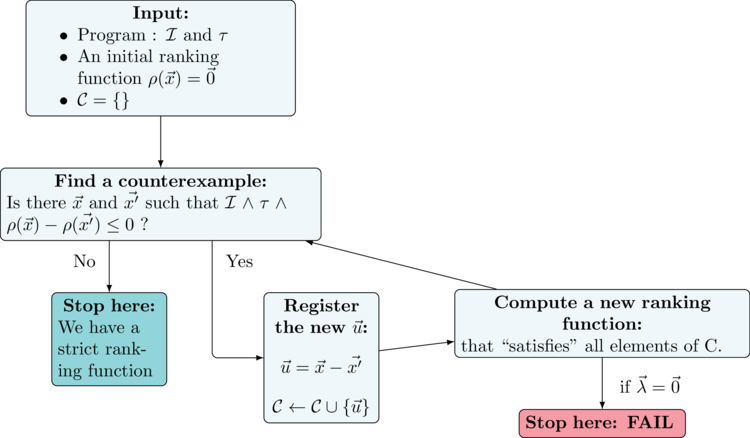
Fighting against scalability : counter-example guided iterations