Une matrice stochastique

> restart:with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A:=matrix([[1/6,0,1/3],[1/2,1/2,1/3],[1/3,1/2,1/3]]);

Caractérisation des matrices stochastiques

> evalm(vector([1,1,1])&*A);

Forcément... cela traduit exactement le fait que la somme sur chaque colonne vaut 1.

> evalm(A^50);

> evalm(vector([1,1,1])&*A);

Ainsi, A^50 est stochastique

A-I3 non inversible...

La relation de la qestion précédente, une fois transposée, nous dit que t(A)-I n'est pas injective donc par inversible. Il en est donc de même pour t(t(A)-I)=A-I...

> I3:=Matrix(3,3,shape=identity);

Ben oui...

> kernel(A-I3);

> colspace(A-I3);

A^100 et A^200

> map(evalf,evalm(A^100));

> map(evalf,evalm(A^200));

Tiens tiens...
Au fait, comment Maple fait-il pour calculer A^100 ? Plus précisément, il fait combien de multiplications matricielles ?

Un polynôme annulateur

> B:=evalm(A^3+a*A^2+b*A+c*I3);

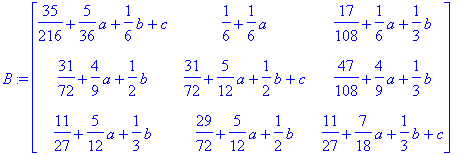
> eq:=seq(seq(B[i,j],i=1..3),j=1..3);

> solve({eq},{a,b,c});

> minpoly(A,X);

Cette fonction magique sera expliquée... l'année prochaine en maths.

> P:=X^3-X^2+X/36-1/36:

> evalm(subs(X=A,P));

Calcul de A^n

> factor(P);

Le reste dans la division de X^n par P est de la forme dX^2+eX+f : on trouve d e et f en évaluant cette relation en les racines de P :

> solve(P);

> S:=solve({1=d+e+f,(I/6)^n=-d/36+e*I/36+f,(-I/6)^n=-d/36-e*I/6+f},{d,e,f});

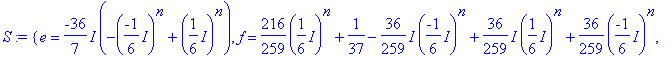
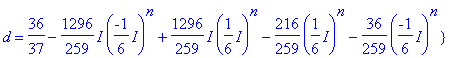
> assign(%):

> evalm(d*A^2+e*A+f*I3);

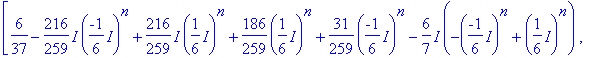
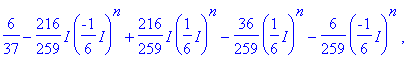
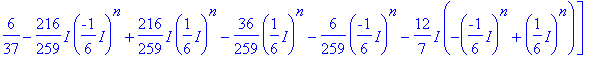
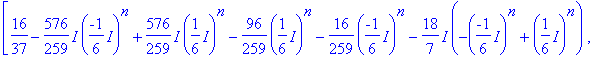
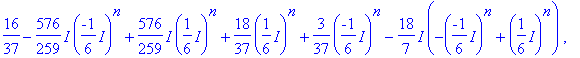
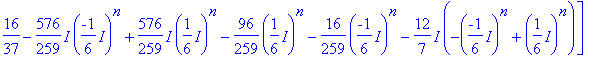
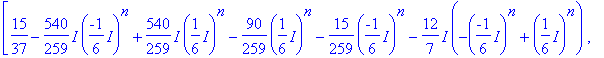
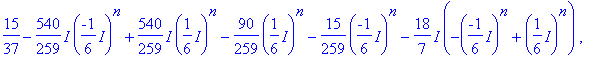
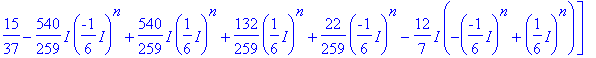
> evalm(subs(n=50,%)-A^50);

"Limite" de A^n lorsque n tend vers l'infini

> d,e,f;

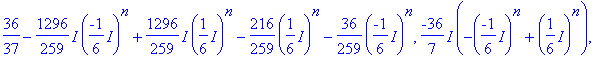
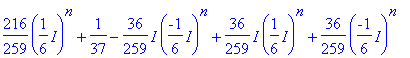
> limit(d,n=infinity);

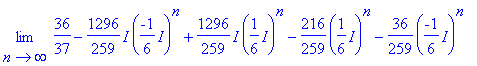
Tsss...

> d_inf:=36/37:e_inf:=0:f_inf:=1/37:

> B:=evalm(d_inf*A^2+f_inf*I3);

> map(evalf,B);

Voir la troisième question...

Propriétés de la limite

> evalm(B^2);

Ainsi, B est un projecteur.

> evalm(A&*B),evalm(B&*A);

B commute bien avec A. On peut le montrer en passant à la limite la relation A^(n+1)=A.A^n...

> colspace(B);

C'est le noyau de A-I. Déjà, si AX=X, alors A^nX=X pour tout n, puis BX=X, donc X est dans l'image du projecteur. Réciproquement, si X est dans l'image de B, alors BX=X, donc ABX=AX, mais AB=B, donc ABX=BX=X, et ainsi AX=X.

> kernel(B);

C'est l'image de A-I. Preuve ? Déjà, au niveau des dimensions, le théorème du rang appliqué à B et à A-I nous assure que ça marche. Il reste à montrer une inclusion : à vous de jouer !